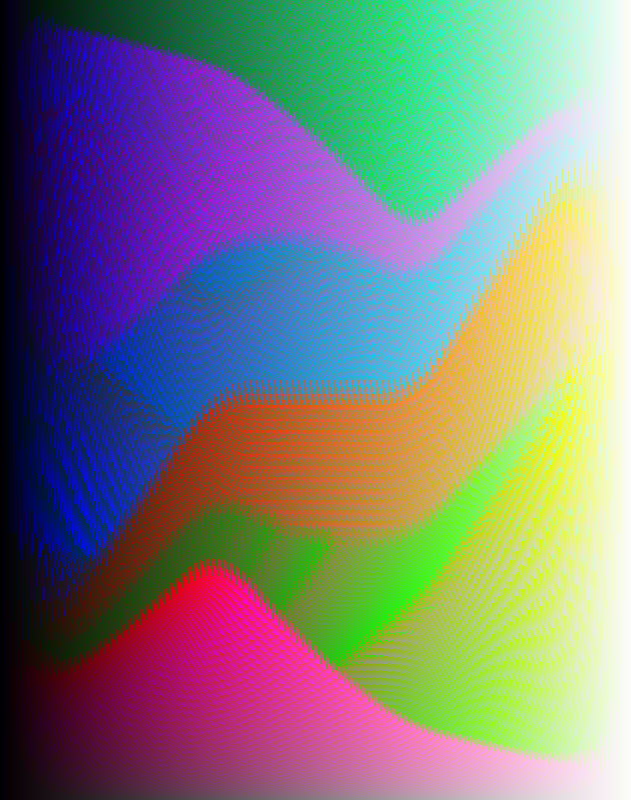Color Pickers

November 29, 2009 by Lukasz Strozek

(Originally published on November 29, 2009)

I bet you've seen color pickers before. They are neat UI elements that allow you to select a particular color that you may have in mind. They do that by organizing the entire color space in a way that's easily browsed. Usually, pickers show you a 2D panel that displays all colors along two of the dimensions, and a slider for the third dimension; or they only show you a small-ish subset of all the colors.

I’m fascinated with color, especially when there’s math or technology involved. And so I set out to build a picker that displays all the colors, yet requires only a single two-dimensional surface.

The color space is three-dimensional: to uniquely identify a color, you have to specify three dimensions. There are many ways to specify a color: the most common one (albeit not the more natural one to understand) is the RGB space: each color is identified by the intensity of pure red, pure green and pure blue components that, when mixed together additively, construct the desired color. I emphasize additively because when we think about “mixing” color (when we paint with oil or watercolor) we don’t actually compose color the same way our eye does. In the RGB space, there are three numbers you specify for each color: and so yellow can be defined as (1.0, 1.0, 0.0) because it consists of max intensity red and green and no blue. Violet (like the color of this flower) can be defined as (0.6, 0.3, 0.7).

Similarly, there are other ways to describe a color: the HSL space, that I find fairly intuitive, describes a color by specifying its hue (the location on the rainbow), its saturation (how vibrant is the color) and lightness (how bright it is). Again, three dimensions (why the color space is three-dimensional is an interesting question…).

This fact makes it hard to design user interface elements that allow you to pick a color (color pickers): the screen is two-dimensional so you either need a slider or some other way to change the third dimension, or you will see a selection of all colors. Being a visual person, I wanted to have a picker that displays all the colors at once, without some stupid slider.

My first attempt took advantage of the fact that on a computer, every measure is discrete (there is no such thing as infinity in computing) so I can collapse the three dimensions into two simply by cleverly rearranging where each colors should be placed. Assuming that each color component has 256 degrees of intensity (which is the case in computer screens these days), we can list all colors, for example

(0, 0, 0), (0, 0, 1), …, (0, 0, 255),
(0, 1, 0), (0, 1, 1), …, (0, 1, 255),
…
(255, 255, 0), …, (255, 255, 255)

We can now map the sequence into a two-dimensional one, for example

(0, 0), (0, 1), …, (0, 4095),
(1, 0), (1, 1), …, (1, 4095),
…
(4095, 0), …, (4095, 4095)

The problem, however, is that we want the mapping to be smooth, i.e. ideally we would like nearby pixels to have similar colors, and the mapping above (and in fact most mappings) won’t guarantee this.

This is where math comes in handy, specifically the field of space-filling curves. I kept one dimension (say, the blue component)–that will be my X coordinate of the resulting picker. For the other, I used a Hilbert-like curve to collapse the green and red components into one Y coordinate. A nice thing about Hilbert curves is that they are somewhat smooth: in this picture, if you pick two neighboring points they are likely to be close to one another on the curve. I’ll leave as an exercise for the reader to determine the actual expected Euclidean distance in color intensity for randomly picked two neighboring points on a Hilbert curve.

Well, such was the first experiment. The resulting “color belt” was very long (because collapsing two dimensions into one makes it a very long dimension!) and the lack of smoothness was pretty obvious :

My first approach to create a two-dimensional complete color picker

I then took the belt and made it into a ring, by “curving” the long dimension around (to take advantage of the fact that the circumference gives me 2π more space than the radius:

Besides looking very Tolkenian, the ring has a pleasing æsthetic to it. Still, it’s somewhat hard to pick out the color you want because the colors are fairly scattered (if your mouse if off by one pixel you may be picking a totally different color).

The next approach was to be a little smarter with the choice of dimensions. Instead of picking one of the components to be one dimension and try to collapse the other two, I chose the light intensity of a color as the horizontal dimension and then collapsed all colors of a given intensity into the vertical dimension. The advantage of this approach was an increased smoothness: all colors along a vertical line had the same intensity; and because the intensity function is linear in the values of R, G and B (it’s a weighted average of the red, green and blue intensity), the colors on a horizontal line are all similar.

I also varied the order in which colors would be placed on a vertical line, based on a heuristic of the R, G and B component. Some of the choices gave very interesting results. Some of these pickers are shown in the gallery below, in order:

Image 1. Plotting each vertical line based on the lexicographical order (sort by R, then G, then B)
Image 2. Making the heuristic slightly more complex: ordering the pixels by the value of the sum of squares of the colors
Images 3 & 4. Bundling similar colors together (to have fewer “boundaries” where neighboring colors differ significantly at the expense of more pronounced boundaries): I used a heuristic that “favored” one component over another.
- Specifically, for Image 4: In first order, pixels whose B is higher than R appear higher in the image. Then pixels whose G is higher than B. Finally, pixels whose R is higher than their G
Image 5. Pixels ordered by saturation - funky!

Finally, massaging one of the above pickers slightly (to eliminate some of the more obvious artifacts), reducing in size and despeckling (to make picking more accurate), and with a pure gray gradient on the side for easy reference, we get the complete yet two-dimensional color picker:

No such thing as a free lunch

November 28, 2009 by Lukasz Strozek

The other day, a friend of mine wanted to use technology to automate some reports he needed to generate. I described to him the options he has: he can either put the time to find (and to learn to use) the right tool that empowers the non-technical person to create reports, spend money on a consultant who can whip the reports, or duct-tape something himself but understand the consequences of such a myopic solution (e.g. it gets very difficult to maintain the reports after they reach certain complexity, easy things are very easy but hard things are impossible, etc.). He asked me something that at first stunned me; he asked “why can’t this be done fast/cheaply and well?”

One of the most difficult things for non-technical people to understand is that technology solutions are expensive. Worse–many technology solutions that seem like they should be cheap are expensive. Essentially my friend came up against a classic problem of technology and software development: what is easy to describe/visualize is often very difficult to code up. For that reason, making technology that empowers business users is expensive because small changes in business requirements may lead to large changes to the software. We are therefore left with two poor options: to spend a lot of time/money up front building something that is flexible and operates on concepts familiar to the user (as opposed to some technical conventions), or to continue spending even more money building one-off solutions.

There are two dimensions that people usually care about: time and cost. Everything else (quality, flexibility, user experience) can be expressed in terms of these two dimensions. You can trade one off against the other but you can never lower both. In other words, there is no such thing as a free lunch.

At this point, I reflected on one point that I used to consider as counterarguments to the above: what about quality? Surely there must be some advantage to hiring a smarter software engineer, or one that understands the business user better.

True, there is an advantage, but it comes at a cost. Quality is nothing else but aninvestment in a solution that makes future changes (or troubleshooting) easier. It can manifest itself as code that is written more cleanly, adhering to accepted best practices (so that a future developer can understand the code easier and thus make changes faster), or more flexible (so that less code needs to be rewritten if the requirements change), or more user-friendly (it takes the users less time to use the tool). High quality code will cost you less in the long run, but it will cost you more today: you will have to hire an experienced developer, or a smarter one (one who has the gift of foresight), or have them spend more time (=money!) understanding the business so that the user experience is improved.

Many startups bias themselves toward time-to-market: getting something out today that works today. As those companies grow larger, technology becomes more convoluted (and thus harder to improve) because a lot depends on this poor quality code that the early technologists wrote to solve the problems of the day. Ultimately innovation is stifled because even the smallest changes become risky and nobody wants large system overhauls without a clear ROI, especially that what is already in place works.

This dead end is caused by two compounded factors: the business people have a myopicunderstanding of value and cost, and the technology people have a hard time assessingeither. So if you have a startup, ensure that your technology people can tell your business people how much something will cost, not today, but in its lifetime (this includes an assessment of a lifetime of a particular solution–nothing lasts forever!) and ensure that your business people can make decisions based on the long-term as well as the short-term view.

The right answer is somewhere in between. It would be dumb to spend a lot of money building extremely flexible solutions because fast time-to-market is crucial in a startup. But invest some money up front (by either hiring smart engineers and experienced engineers–you need both–or introducing governance) and build in guardrails that make it cheaper to make changes in the future.

The consulting industry and entropy

November 26, 2009 by Lukasz Strozek

I like entropy because it’s such a simple concept that’s easy to define (a measure of disorder) and universal (it looks the same throughout the universe). Its definition doesn’t depend on other words that can be loaded (such as “happiness” or “language” or “intelligence” or even “evolution”) so it’s a good term to use as the basis of a framework for thinking about life.

Entropy in the thermodynamic sense has a close equivalent in the field of information theory. In fact, its equivalent is so close that it’s also called entropy. It is a testament to the universality of the concept — in fact, I truly believe that I could define everything I can think of in terms of entropy. Perhaps one day I’ll publish a dictionary that does precisely that.

In the meantime, my friend, wishing to see me suffer, challenged me to define a seemingly unrelated thing in terms of entropy. Here it goes.

I’m intrigued by the consulting industry, specifically management consulting. At first I had a somewhat cynical view of it (in fact, as I saw many of my friends prepare for interviews that seemed to ask nothing but Fermi problems. Ironically, most of my friends didn’t know they were Fermi problems… here’s a cheat sheet if you’re preparing for a consulting interview). I interacted with consultants at work (and saw the best of them in the movie Office Space) and found it very difficult to understand how they can be adding any value. After all, they don’t bring any skills to the table. Most importantly, there was an unsettling stench of slickness to many of the consultants I’ve interacted with, almost as if every conversation was a game to be won or lost (or–again, taking a cynical view–as if it was through the slick conversations that the consultants were making an impression of adding value).

Then I thought about it some more, in the abstract, starting from what I imagined to be the history of consulting. I had this impression of the consulting industry as being pioneered by a few incredibly smart people (university professors perhaps)–I call them “founders”–who worked out through the theory of efficient management, information flow and social interations and determined some theoretical framework that they published in a seminal work in the mid-1950s. Following them were ambitious and innovative entrepreneurs who decided to put their theory in practice–they worked out the kinks that usually prevent the elegant theory from being applied to the real world (this is also probably the reason why we hear about groundbreaking research in battery technology yet nothing seems to reach the mass market). I call these people “visionaries”. They came up with principles and set up the first consulting companies. Over time, as it always happens, the principles were lost and the companies lost sight of their mission and their roots; it all became a matter of making money (incidentally, this happens to a lot of industries which is why sophisticated enough companies all look the same, regardless of what they do). Surely, then, in theory consultants add value, even though what we see today obscures it well. Let’s find it (and let’s use entropy to explain it!)

Entropy in the information theoretical sense measures how much information some data contains. A string of zeros: 0000000000 contains no information while a random string of zeros and ones: 001101001011101 contains plenty of information. In other words, entropy tells you how predictable the data is. We can also talk about entropy rate–a measure of the “density” of information. For example, English text has an entropy rate of about 1 bit per letter, which means that if you were to represent English in the most efficient way (but without losing any information), Shakespeare’s Romeo and Juliet would take up about 169 thousand bits. Note that the most popular representation of English today on a computer is to use ASCII (assign an 8-bit sequence to each letter) at which point the same play would take up about 1.3 million bits in such an encoding–the amount of information varies depending on the encoding and this is why entropy assumes you find the most efficient such encoding.

Of course entropy rate depends very much on the domain of the information. While entropy rate of English is 1 bit per character, entropy rate of, say, the scripts of soap operas is much lower than that. It’s because what is said in soap operas is much more predictable–fewer sophisticated words are used.

While it’s hard to find the theoretically correct value for the entropy rates of data, a good first-order approximation is to compress it using a good lossless compression algorithm (for example, make a zip of the data) and look at the compression ratio. For example, Romeo and Juliet takes up 165kB (which translates to the aforementioned 1.3 million bits). Once you compress it, the text takes up 63kB. The compression ratio of 38% means that the entropy rate of Romeo and Juliet is about (38%*8 bits per character that ASCII uses) = 3 bits per character. More than regular English, but, there again, Shakespeare is a little less predictable than your average Joe (plus, there’s overhead of the compression program itself, and it’s not ideal, too).

Now the punch line: consultants are often brought in to synthesize information and come up with recommendations. While the recommendations are usually commonsense, the synthesis is hard. They have to interview lots of people, look through reams of documents, stare at various charts and graphs. This is a lot of information. At the end of their engagement they come up with a powerpoint document that summarizes the important findings. It’s usually an incredibly dense powerpoint — carefully chosen words, terse bullet lists, not even full sentences, articles and prepositions are the first ones to go. If they’ve done the synthesis right, they were able to fairly losslessly (given what they were supposed to recommend on) compress the information into a powerpoint. Hence, the way to assess the value of their work, simply find the entropy rate of their deliverables. High entropy means high value.

You don’t even have to bother reading the powerpoint document!

The greatest moment in my lifetime of interactions with computers

November 24, 2009 by Lukasz Strozek

For those who prefer brevity to beauty, here it is: the day I discovered DOS/4GW. For everyone else, read on.

Thanks to my dad’s wonderful prescience, I grew up with computers–and by grew up, I mean grew up. I think the first computer in the house was a Commodore (although for some reason I imputed a memory of my dad owning an Amstrad-Schneider). I was too young to remember much other than sitting on my dad’s lap and staring at the computer screen. Back in the day it was impossible (and I believe also illegal) to own “imperialist” equipment (I know one needed the governor’s permission to get a car) and so I am deeply impressed by my dad’s ability to do magic.

When I was six or seven (again, I don’t remember exactly), I got my very own ZX Spectrum + with a black-and-white monitor. I remember playing with it for hours (the fact that those years spent staring at a CRT screen haven’t made me blind confirms my theory that if you grow up with something you get used to it and it doesn’t harm you; ironically many of my friends who got their game consoles or computers when they were teenagers are nearly legally blind now).

Pretty quickly I started writing programs for it. Looking back, this was crazy–the user manual was in English and so at age seven I knew about eighty words–keywords used in programs I’d write–in English very well but no grammar or vocabulary that kids my age for whom English was their native language knew (a fascinating way to learn the language).

I don’t want to digress too much from the theme of this post; one day I’ll continue the rant. The important thing was that at the time the computer had 48k of memory available (an equivalent to the amount of information contained in the text of the Constitution of the United States of America; to put things in perspective, computers come with 2GB now, which is about 40 thousand times more). I didn’t feel I needed much, though, because the capabilities of the computer were limited and my brain was pretty small, too. Over time, however, I did start bumping into these limits more and more. I could define my own characters and sprites (for which I had to learn to operate in binary; knowing binary before I knew how to divide is a funny thing, now that I think about it) but I could define at most 256 of them.

Fast forward six years, to my first PC (getting close to that ominous greatest moment). Eternally curious how to make games rather than play them I’d continue programming. My brain, now more fully developed, could process more information and so I expected my programs to. The PC was also capable of much more (I think I had 16MB of memory at this point?) yet due to the hardware limitations I could use at most 640kB of it. You may think that a little more than 650 thousand bytes should suffice but that’s how much information is contained in a single uncompressed photo! I felt very constrained–my computer could play sound, display graphics, and perform calculations much faster than anything I’ve seen before. Yet I couldn’t take advantage of any of it. There seemed to be some kind of a rule that stipulated those omnipresent limits–party poopers. There seemed no way around it.

Then, one day, I discovered this utility called DOS/4GW. It wasn’t a discovery as much as a result of an investigation: I’d see more and more advanced games pop up that surelycouldn’t have been subject to the 640k limit (they combined music with graphics and seemed to store a lot of information about the virtual worlds they were depicting… my intuition told me that must have been more than the measly 640k). All these games would launch a small application before they themselves started, and that application would simply pop “DOS/4GW” on the screen and disappear. So I started digging.

I found out (at that point I didn’t have any access to the Internet–searching for information was so incredibly painful back then) that this little utility allowed the game programmers to bypass the 640k limit, effectively taking advantage of all the memory that the computer had available. And to my shock it turned out that I could also take advantage of this application when making my programs.

This lifting of the limit was, in retrospect, the single most eventful day in my entire life of interaction with computers. For one, the limit was immediately increased from 640k to 16M (a 25-fold increase!). But, more importantly, it was a soft limit: I could simply buy more memory and have more available to my programs. I felt empowered*. I went crazy–there were finally no limits to my creativity.

* What I didn’t know was that DOS/4GW didn’t abolish the limit altogether; it simply upped it to 4GB. But given that most of us don’t have that much memory even today, that fact wouldn’t have registered with me as something fundamental then. Now it’s part of the sad reality about modern computing–it’s all painfully finite.

How to Prioritize Things

November 19, 2009 by Lukasz Strozek

Prioritization is a difficult problem because it involves more than one factor. If only one dimension is important, prioritization is easy: since prioritization is an ordering of things, all we need to do is come up with a consistent (transitive, i.e. if A is “more” than B and B is “more” than C then A will always be “more” than C) ordering of items based on that one factor. For example, if we want to prioritize solely based on how much we want to do something, we’ll do a good job coming up with the order (do it the way we sort a hand of cards — for each item, figure out which of the items already prioritized it’s “more” than and which one it’s “less” than).

The reality is that prioritization involves multiple dimensions: how much we want to do something (both in the short term–instant gratification–and the long term), how long it’s going to take, how hard it’s going to be, how tedious it is to do (which is different from the other three!), etc. We can no longer come up with orderings because we don’t really understand how the different dimensions relate to one another. Which do I want to do first: something that takes a long time but is enjoyable, or something that’s hard but gives me something in the long term (and, of course, the degree to which these factors are at play is also important).

I’ve witnessed many people try to come up with frameworks to handle this problem. We’ve all done it: one-to-ten grades, complex formulae that look like weighed averages (although nobody wants to admit that that’s what they are), forced rankings, baffling heuristics… I’ve tried and failed many times. At the end of the day I feel like something is not quite right.

And this led me to a solution which I’ve been trying out for the past two weeks, with great success. I started prioritizing things based solely on one factor (which is easy), namely based on how anxious not doing them makes me. I think I’m “spawning” a new principle that seems a good one to follow in my life: leading an anxiety-free life (perhaps that’s what happiness is, after all).

I have a short list of problems that I want to tackle in my life. I reorganize this list based on how anxious I feel about each of these problems. All tasks that I have to do that derive from these problems are therefore much easier to prioritize. While this model is much more simplified (it ignores a lot of the factors I mention above), I’ve found it to be (a) very satisfying, and (b) fairly robust (i.e. I can still shuffle some of the tasks around and by and large I feel good about the results). Perhaps this capacity of something to reduce one’s anxiety is a good natural heuristic that combines these factors. Perhaps it works because it addresses a deep feeling, a kind of fundamental utility. Either way, it works like a charm.

The perfect language

November 12, 2009 by Lukasz Strozek

There have been very many attempts to construct languages. Some of them–mostly ones to construct computer programming languages–have succeeded. While it’s been tempting to come up with a perfect human language (“perfect” defined in many ways: free of ambiguity, efficient, aesthetically beautiful), such attempts have failed.

Why is it so hard? It has to do with how humans utilize language. Language is a reflection of the way of thinking, and we think in a fuzzy way, so the language is fuzzy. If we try to make it precise, we’ll struggle to convert our thoughts into language.

A good example of this conflict is Esperanto. Zamenhof intended to have a language that’s perfectly phonetic. People struggle with the duality between spelling and pronounciation all the time, so why not solve the problem at the outset? It turned out to be an impossible mission. Exceptions to rules would appear (seemingly out of nowhere) as soon as the language was released and started living its life.

This is directly related to the fuzzy thinking that happens in our brains. We don’t just abide by strict rules of grammar; we implicitly trade off the consistency of structure (which is rigid) against the freedom of antistructure (which creates exceptions). It’s as if our brains were picking the most efficient representations of our thoughts.

Why are efficient representations not always structured? For example, why can’t language employ a Huffman-like encoding where frequently used concepts have “short” representations? It’s because we don’t know ahead of time what we will use frequently and a high cost of internalizing a representation means our brains have to pick the representations opportunistically. Greedy processes, such as this one, often create unstructured systems.

If you don’t believe that an ideal human language cannot exist, consider analogous systems, for example the organization of information in a workplace. I’m baffled at how little sense things we see at work make: information seems to be scattered everywhere, there are no standards for where to store documentation, links between sources of information are broken. It’s a particularly big pain when I try to apply a precise framework to the problem of information retrieval: for example, when I want to automate processes that operate on information. Naïvely I say to myself that if I had started all over again, information would be organized well and be easy to find, links would be maintained, standards in place would drastically reduce the complexity of solutions needed to tie all the information together. It’s a naïve view because that would be an incredibly inefficient approach (small systems benefit from unstructured solutions; as the systems get big, there are too many exceptions to come up with a good systematic solution).

This conflict between an efficient short-term (micro) solution and an effective long-term (macro) solution occurs all over the place. For example, game theorists know of many cases of games where locally optimal solutions are at odds with globally optimal ones (say, prisoner’s dilemma). The problem occurs because of lack of information: in the case of language, the brain doesn’t know what representation will be used frequently; in the case of technology it’s unclear what kind of standards are needed (implementing standards for standards’ sake is wasteful); in the case of prisoner’s dilemma, the prisoners don’t know if they can trust one another. There is no good solution.

Which is also why there will be no perfect language.

The Metric system vs the Imperial system

October 25, 2009 by Lukasz Strozek

This must be the most popular topic of conversation whenever a bunch of Europeans get together...

The U.S. adopted the English system of measures several hundred years ago and while the rest of the world (including Great Britain) moved on, going with the Metric system instead, we stuck with the good old pounds, inches, and ounces. As is the case whenever an entity used internationally lacks international standards, it's been causing loads of confusion and even disasters. Besides asking why this is so (the United States is uniquely insular in this respect, even more than actual islands such as Japan or Great Britain where such a thing would have a natural justification), a lot of people engage in the oft time-consuming and fruitless rhetoric of which system is superior. I'm going to add to this hairball, but only a little bit. And I'll try to use first principles rather than dogma (we'll see if I succeed).

The goal of having a standard of units are to provide a common framework for the society to efficiently and robustly (i.e. in a way that's resilient to errors) convey information about measures that doesn't require special skills (i.e. to make the framework usable by as many people as possible).

I think there are two factors one must take into consideration when comparing the two systems: the intrinsic properties of the units (how practical they are in daily use) and the way they can be manipulated and composed (how to multiply them, compare them, convert them). I claim that the Imperial system is superior at the former, and the Metric system--at the latter.

What makes Imperial units intrinsically superior is the very choice of how much a primitive of various frequently uses measures actually measures. I think an inch is superior to a (centi)meter -- I'm sure that if we were to take a survey of all lengths that humans refer to in their lives (controlling for a selection bias--people will tend to round up or down to the nearest unit of whatever system they are using), and draw a histogram of such usage, there would be a peak around the inch and not the (centi)meter. I'm even giving the Metric system the benefit of the uncertainty around which unit specifically should count as the primitive. In other words, we're more likely to talk about things which are the size of an inch than things which are the size of a centimeter. Similarly, the (mili)liter is inferior to a fluid ounce -- a fluid ounce is a more natural measure of a "splash" of a liquid.

There is a second-order effect of measures around, not at the primitive: do things more naturally come in (sub)harmonics of an inch ("half an inch"/"one-quarter of a pound"/"three ounces") or the meter ("three centimeters"/"one-half of a liter"). This is probably much harder to determine. However, one important property of the Imperial system is that it operates primarily on natural and not decimal fractions of units. The Metric system talks about 0.2 centimeters; the Imperial system talks about one-eighth of an inch. Natural fractions are (even by the very definition) more engrained in the human nature than decimal fractions--we're used to thinking about dividing things into equal parts and visualizing individual parts than dividing into a fixed number of parts (10) and visualizing multiples of that fraction.

The most important benefit of the Imperial system, in my view, is that it operates (mostly) on base 12 and not 10. I already wrote about how base 12 is far superior to base 10--it divides cleanly into 2, 3, 4 and 6. Base 10 numbers divide cleanly only into 2 and 5. Having intrinsically more divisors is better because it avoids awkward infinite fractions and, ultimately, inefficient communication.

When it comes to the second factor, though (how the units are manipulated and composed), the Metric system wins hands down. The Imperial system is inconsistent (12 inches to a foot; 16 ounces to a pound); there are far more units to remember (fluid ounce, pint, quart, gallon) and more units to remember the relationship between. The Imperial system captures many fewer measures at the very small and the very large range -- in fact, the only way to represent very small or very large numbers is to use the multipliers that are the very foundation of the Metric system (10 million pounds, for example)!

Most of the disagreement, then (especially when a bunch of Europeans get together...), can be boiled down the the philosophical difference (I define a "philosophical difference" as a difference in opinions that cannot be reconciled with logic because it's simply too costly to find a way to compare the opinions objectively) -- do you prefer the intrinsic properties of the units (which I feel are more aligned with human nature), or the composition properties of the units (which are more aligned with civilization).

How to Diagnose Problems

October 22, 2009 by Lukasz Strozek

The ability to diagnose problems is one of those incredibly useful skills to have in life. From experience and observation, I can say that very few people possess it. While it’s a bit of an art, there are some simple principles that people just don’t seem to apply.

You may think that diagnosing problems is an ability that’s really only useful in a narrow domain, such as programming or fixing cars. But we come across problems all the time, even when we don’t realize it (A clogged drain in the bathroom. Tivo doesn’t want to record your favorite show. You don’t seem to be losing any weight despite being on a diet). So here are the basic principles. Nothing in here will be a surprise to anyone; the bulk of the work is in internalizing those principles–and being able to apply them when solving problems.

Define the problem.
What is the problem exactly? Can you concisely yet precisely formulate what the problem is? If you have to use words such as “broken”, this is usually an indication that you haven’t really defined the problem well. How does the problem manifest itself? It’s very useful not to mix diagnosis with the formulation of the problem; at this point your diagnosis may not be correct and you may be incorrectly leading yourself down a wrong path from the very beginning. A useful trick is to try to simply phrase the problem as something that constrains you, i.e. something that prevents you from doing something.

Replicate the problem.
Can you show me the problem manifesting itself? Most problems in the world are easily replicable; for example, if the TV doesn’t turn on, it doesn’t turn on. But some problems are more tricky than that–maybe your brakes make a noise only when the engine has warmed up enough; if you just turn the car on, you won’t hear the noise. Being able to show the problem occurring is very useful as it allows you to test your theories easily. Note that at this stage you don’t need to figure out all circumstances under which the problem occurs: you just need one.

Contain the problem.
Try to replicate the problem with as simple a setup as possible. This will eliminate a lot of the factors that would otherwise have to be included in the diagnosis. A lot of people either assume that most of the steps they did are necessary for the problem to occur (very rarely is a problem a coincidence of a large number of factors), or assume that most of the steps they did are irrelevant (surprisingly frequently is a problem due to something that one implicitly rules out early in the diagnosis stage).

An Aside: on Theories
Note that while you will certainly run across theories about the problem as you try to replicate it and contain it (and sometimes even define it), you should be careful not to jump to conclusions too quickly. I think a lot of smart people are also lazy, and this combination manifests itself as impatience when diagnosing problems. There’s nothing wrong with having theories, and in fact, experienced diagnosers will be able to come up with a theory with very little information. But what I see a lot is people coming up against a problem they can’t solve and struggling to solve it because they are either stuck with theories that don’t work and can’t find better ones, or went down the wrong path early on in the diagnosis (when I was a teaching assistant in a computer science class back in college, I would help students find bugs in their software. They would be taken aback at the simple questions I asked them; “Of course that’s not the problem,” they would say. I’d tell them, “If everything is an ‘of course that’s not the problem’ yet you can’t fix the bug, at least one of the ‘of course that’s not the problem’s is probably the problem”.

So hold off on theories for as long as you can–if you ran across a hard problem (which is really the domain we’re interested in here), you are likely to want to solve it, and only as a second-order thing to solve it quickly.

Locate the problem.
Chances are, by now you probably will have located the problem to a large extent. If you haven’t, it’s the natural next step: determine where the problem lies. There is only a subtle difference between locating a problem and testing theories, so you will invariably be doing the latter as well. Start with your (small) setup needed to replicate the problem. Vary your setup to draw conclusions about where the problem is (or, more likely, where it is not). This will help you narrow down a set of theories that you will have to try out by a substantial amount. It’s a good idea to do easy things first (to gather as much information as possible about the location of the problem), but of course there’s a bit of an art in trading off cost of the experiment against the expected amount of useful information it will give you.

For example, I once had a clogged drain in my sink. Here is what I did–compare this with the steps above:

The problem was this: the sink would accumulate water quickly so I couldn’t have the tap running too long or I’d flood my bathroom.
I could easily replicate the problem by turning on cold water to its maximum and waiting for one minute. The sink would fill up with water.
I noted that I don’t need to use cold water; hot water would do as well. I also didn’t need to turn it up to the max–at some point (maybe half way through) water would start accumulating
Locating the problem is one of my favorite parts of diagnosis. First, I poured water down the “safety” drain located on the upper part of the sink (the one that prevents the water from spilling out of the sink). I could not replicate the problem. This means the problem is somewhere between the hole in the sink and the part where the drain meets the safety drain. This is great because I no longer needed to unscrew the “U”-shaped part in the drain (it was below where the safety drain flows). If I had started with a theory (“there’s probably a bunch of disgusting stuff blocking the ‘U’-shaped part”), I would have wasted some time.

Note that normally we just do this all implicitly, in our heads, but there again, a clogged drain is not a hard problem. It’s a good idea to be a little pedantic once to get a feel for what diagnosing problems well means.

Finally, form theories and test them out
If you’ve gotten to this point, you are likely dealing with a hard problem. Good!–because this is where the most art comes in. The hard part about forming theories is that you have to find theories that help you prune your search tree as much as possible, in as cost effective way as possible.

The “search tree” thing is very important. I cannot stress it enough. Each theory you test eliminates a class of problems. So if you imagine the set of all possible problems, each theory you test in the sequence will eliminate a subset of them. It’s much better to eliminate most of the problems first (this gives you fewer problems left, so fewer theories to test). It’s a little bit like the game of 20 questions–it’s better to ask a generic question that eliminates half the possibilities first, than a specific question that with high probability eliminates a very small set. Of course you don’t know the probabilities or even the eliminatory power of your theories so this is where the art comes in. You have to trade off three things:

How expensive is it to test your theory?
In the best case, how many problems can the test eliminate?
How likely is the best case?

Again, if you’re stuck with a problem, you will likely not care about being the most efficient so really you should strive for your theories to simply eliminate as many potential problems as possible (ideally in a balanced way, just like the questions a good “20 Questions” player would ask).

The nice thing about a problem tree that you thus construct is that if it’s balanced, you will not need to test many theories — just like 20 questions should be enough to find a thing from amongst a million things! However, one thing I see people do over and over again is forget where they were on the tree and either redo many tests, thus getting no useful information, or perform tests that are irrelevant given where in the problem tree they are (for example, if I tried to see if the “U”-shaped part is clogged after I figured out that it’s not the problem).

What being 25 years old taught me

October 20, 2009 by Lukasz Strozek

The thought that resonated the most in my mind as I was turning 25 was that two years had passed since college and I hadn’t really been striving for anything. It seemed different than my time in college, which was filled with non-academic activities. I didn’t want to become complacent with life, just kind of let things go, in fear that I would let my life crawl past me.

The result of that thought (fear) was the plan to achieve 25 things while I’m 25. Half way through the plan, I changed it to be less a random collection of items and more like a goal tree, each goal being derived from the few things that I really cared about. What I really cared about then were two things: knowing what my purpose in life is, and proving to myself that I can execute on goals. Now that I’m no longer 25 it’s time to retrospect.

A question that people have been asking me for a while now is “so how many items did you achieve from the list?” It’s a good question; it gives one an idea of either my follow-through, or my ambition (or both). I did 15.

I will focus on those achievements that I think taught me the most. For one, several of the goals had to do with a behavioral change, something that’s overall very difficult to do and usually takes a lot of time. I started leading a much more active life (running the half-marathon–and the marathon, but that was after I turned 26–and taking up swimming were examples of the goals which required the change; I also did some crazy things like bike to Manhattan and run to work, which was fun). I’ve gotten to the point where the default modus operandi is for me to go running, or swimming, or biking — without it I feel like my day isn’t complete.

That one was the most striking example of behavioral change. There were other goals in that category, which I achieved, but which still don’t feel natural. Reading is one of them (my goal was to read 50 books). I also vouched to be less angry at people (and things), and to deepen my friendships with people I care the most about.

Another big achievement was beginning to think. I realized that I haven’t been thinking nearly as much as I should have been (in general, I realize I should adopt a philosophy of contrasting my thinking and my doing–letting one feed off the other, and improve based on the other. Too much doing caused me to stop learning, to waste time doing the same things over and over again; but if I let the pendulum swing too much and just think, I’ll lose the much needed feedback that I can only get by applying my thoughts).

Specifically, I started thinking more seriously about my life’s purpose and while I haven’t achieved the overarching goal (of determining my goal in life), I went very far from where I was a year ago. Starting a blog–and holding myself accountable to updating it regularly–helped a lot; I was able to give shape to many thoughts I’ve had around the life purpose, and in general around metareasoning.

Finally there were goals which had to do with changing my perspective, doing something unusual, committing to something that may not necessarily be something I’m most comfortable with. Summiting Mount Kilimanjaro, becoming a regular at a bar and going racing on ice in Colorado were examples of such goals. To release elevenseconds.com I started using ruby. I made myself drive stick. I came to terms with owning a car that’s not quite practical.

What was the outcome of all this? First of all, I feel like I haven’t wasted a year (curiously, the year seemed to pass much more slowly than my twenty-third and twenty-fourth year… I felt fully in control of my life, which I don’t think I could say about the previous two years that have kind of passed me by). I started thinking more (which should hopefully help me figure out my purpose in life, one of those days…). Overall I feel that I’m less anxious (having a site/blog means that I can start sharing out what I’ve done and thought about; having started hard things means that I can still adapt).

The next frequently asked question is “what will you do for your 26th year?” No, I’m not going to be trite–there will be no 26 things. Instead, I will focus on some remaining things, high-level goals that I didn’t get to that still cause some anxiety. By and large I want to focus on:

Being creative — I haven’t gotten to do many of the items on the 25 list that dealt with creativity, and I feel that I don’t really have an outlet for creativity these days
Doing something that lasts — I want to apply the “step back” test when I’m turning 27
Being flexible — this means both in terms of being able to change (continue working on behavioral change–make reading a natural thing, continue leading an active life) and in terms of starting new things, particularly hard things (do miniprojects on weekends)
Figuring out my purpose
Exploring more, seeing more, experiencing more — doing things from my bucket list
Sharing — there’s still so much that’s in my head (and on my computer) that I want to share with everyone

Experience vs Flexibility

October 14, 2009 by Lukasz Strozek

Experience and flexibility are two qualities that seem to be complementary in most people. When we’re new to something, we explore it, we experiment. We don’t mind being inefficient — after all, learning requires some inefficiency (for example, education relies on a principle of redundancy, which is by definition inefficient) because of the uncertainty of the outcome: we don’t know what precisely will allow us to learn how to multiply two things together, so we do it a lot, and we approach it from many different angles. We’re inexperienced but flexible.

As we gather our experience, though, we stop experimenting. We realize that we’re more comfortable with some aspects of whatever domain we’re interested in and not others, and choose not to be flexible. This choice, granted, is usually implicit (nobody just wakes up one day and decides to listen only to 80s music from now on) and gradual, but I think it’s still a choice we make.

I think there are two misconceptions about experience and flexibility. First, the transition from flexibility to inflexibility is seen as inevitable, just like the transition from lack of experience to experience. At work I’d complain many times that experienced hires find it difficult to learn new things, or new approaches, and are often dogmatic. I think this transition, while consistent with human nature, is not a forgone conclusion. It’s still achoice we make, hence yesterday’s post encouraging everyone to explicitly choose not to become inflexible. Secondly, experience (and thus lack of flexibility) is equated with age. I don’t think it’s necessarily true–some people acquire experience faster than others (I guess we call such people “mature”). There are many factors that come into play here–the ability to retain information, the ability to make connections, the ability to reflect.

Why do people choose to become inflexible? I think it stems from the desire for humans to seek comfort. Most people are rational enough to understand the benefits of investment (trading off utility today for much more utility tomorrow: the loss of utility today manifests itself as pain and lack of comfort) but there are limits to how much they want to invest. At some point we naturally gravitate towards reaping the benefits (perhaps as we perceive the passage of time, i.e. get impatient).

I remember fearing that at some point in my life I will stop being flexible. I worried that just like my grandparents find it difficult to operate a remote control, and my parents find it difficult to use a computer, I will at some point “lose it”. Then I would explain to myself that such a terrible thing won’t happen to me because my generation is special in some way — I was born in an age of technology boom, used to progress (whereas my grandparents grew up with the invention of a telephone, television, etc., I grew up with a concept of invention in the abstract so my skills are more transferable across inventions). In retrospect, I think this was a naive understanding. Sure, maybe technology is something I won’t “lose” (particularly because so much of my life revolves around it), but there will certainly be something else that I will not be able to master, or learn, or even understand.

In fact, even us staying on top of technology is not quite so certain. Here’s a great example of how we all ultimately choose comfort (as a result of experience), at a sacrifice of flexibility. My generation (I guess these days saying “generation” isn’t enough–one has to be more granular than that–so, say, people born around 1982-4) prides itself on being very familiar with technology, particularly computers, the Internet and many of its artifacts (such as the phenomenon of social networking). We all poke each other on Facebook, gchat each other at work, subscribe to others’ RSS feeds (ehm ehm). So are we special, at least with respect to technology? Very few (it any) of my friends use Twitter. They see it as “a waste of time”, something “immature”, something that “high school kids do”. Why use Twitter if you can update your status on Facebook? Who cares where you’re having breakfast? Twitter, at least to my micro-generation, is not a basic building block of social interactions. Yet Twitter is incredibly popular. So is it, perhaps, that we’re simplyslightly out of the loop with technology already? Oh sure, we’ll say, we can always start using it. But it’s not worth it. We’ve just chose comfort over flexibility, just like our grandparents did when they refused to learn to operate a remote control.

Back when I used to worry about things, this was a big bummer. Now that I learned to embrace changes, I’m fascinated by this process and want to learn as much from it as possible. What’s the next big thing going to be? We’re bombarded by information; just to stay afloat I’m finding myself going through two hundred posts a day from the thirty or so blogs I subscribe to. It’s time-consuming (and most of my friends have already given up; the smarter ones simply ask me to synthesize the information for them, but that’s a superficial way to try to capture this information–it’s like reading about how Twitter works in the New York Times) and… well, painful. But to others–to the little ones–it’s natural. My friend was telling me how his five-year-old picked up his iPhone and navigated it without the slightest trouble. It’s a great thing, a visible sign of progress. Let’s not get angry, or depressed about it. After all, we were making fun of our parents, too.

What kind of boring blog would this be if it didn't talk about cars!

October 09, 2009 by Lukasz Strozek

Back when I was little I would hear the members of my family (mostly men--but I'll get to that) discuss cars all the time (in between conversations about politics and sports). When I went to school, I would hear kids my age talk about cars. There were even those playing cards you could buy that allowed you to play games with other people by comparing various characteristics of cars.

I never understood that fascination that everyone around seemed to have about cars. Granted, I didn't really know much about cars, and my parents didn't get a car until I was a teenager, so I didn't have much exposure. Still, talking about it seemed like a giant waste of time.

As I learned more about the world around me, I found a spectrum of opinions that people had about cars and car ownership, and discovered that meta-opinions -- opinions about views people hold about car ownership -- were fairly frequent (I guess this post is one of them, huh). Cars were said to be a reflection of their owners' insecurity or vanity (I particularly love vanity plates as icing on the cake, but I'll get to that later); cars as a reflection of their owners' need to dominate; cars as a reflection of the society's reach for ever increasing standards of living. Cars as a symbol of independence and means of living. Cars that liberate, impress, inspire, disgust, bore. Cars as symbols of indescribable wealth. Cars from vending machines as a statement of the society's desperate reach for the extremes of consumption. The opinions are countless and diverse, but one thing is certain: cars seem to be talked about or otherwise involved more than many equivalent objects. The reason for this? The car to me seems to have a large capacity for rhetoric -- it's used as a carrier of illiteral information -- because it's an inseparable part of the human culture; because it's indispensable; because it's an extension of our humanity (this is also why we like cars that look like humans).

When I got a real job, I had to drive to work every day. This necessity brought about car ownership and, subsequently, many thoughts and feelings about cars. I suddenly saw how the humanity of the car applies to my small world. The car connected me with others (how else would I be able to get to NYC to hang out with my friends?), allowed me to get to work, helped me in emergencies, sheltered me when I found myself in the City at 5am about to pass out, having to wake up at 8am, offered me its warmth or cool breeze. It was an extension of my body (while many people like to think of cars as giving their owners undeserved or supernatural powers, I thought of mine as extending my reach (I could go faster) and sight (I could see all around me)).

But most importantly, my car gave me a way to express my passion in a simple, effortless way. Driving my car was like sitting in front of a canvas; each trip was a small work of art. Over the few years I had it, I discovered a lot about what I liked in my car and what I didn't care about. Initially excited about the many bells and whistles--push button ignition, headlights that turned where I turned, eventually even power side view mirrors--I slowly deconstructed my passion towards my car to just one thing: the act of motion, the dance I perform whenever I drive.

This is a highly personal opinion. I know a lot of people who prefer a comfortable ride, or things that make driving easier, such as an automatic parallel parking system. Everyone needs to get to a point when they know what they like in a car (and very usually this is a very fundamental thing). I strongly encourage everyone to lease their first car (or intend to sell it after a couple of years); I look back and realize that I knew nothing about myself or cars when I decided on my first car.

Once you are faced with moving on to your next car, I think you should pursue your passion. Purchasing a should not be a result of calculated, detached reasoning. For example, the rational part of my brain would come up with all those reasons not to get the car that I now own. If I had listened to it, I would never have bought the car. But instead, I followed my passion. This made my car ownership something special; and all those problems that my logical brain came up with turned out not to be problems after all--I came up with good solutions without much of a sacrifice.

A great thing about passion is that it is what keeps you going; an even greater thing about logic is that it is robust enough to recover even after you ignore it from time to time. The art of living is to know when to switch between passion (to live a fuller life) and logic (to live a better life).

Why do men seem to like cars much more than women? I don't know; at the risk of being called a summerist, I believe that men's and women's utility functions are different, and this is reflected in what the two genders care about, and, subsequently, what they purchase: men seem to me to purchase fewer items than women do, but the items they purchase cost more money. I have a feeling this can have something to do with how men value consistency and women value compatibility (this may also explain why women have larger wardrobes--the top and the bottom must match; this means that women will tend to need n^2 articles of clothing while men need 2n).

What about vanity plates? Many plates are trite (they include some variation of the owner's name--it's unsurprising given that they are vanity plates but feel a little too much); many employ irony or try to otherwise be funny. Some are clever; some are just aesthetically pleasing. I love spotting them, and trying to figure out what they say about people.

Commercials that look like news broadcasts and what it implies about our society

October 09, 2009 by Lukasz Strozek

I saw a commercial on ESPN the other day that showed a footage of Obama discussing some issues related to the economic situation of the nation at some news conference. There was also a phone number to a service that apparently allowed anyone to "get out of debt." The first time around it took me a while to realize that it was a commercial.

Conversely, a lot of the actual news broadcasts are beginning to look like commercials. News bits are dramatized (remember how Fox used to make its news teasers look like fragments of the show 24? And-come on-news teasers?!). A kind of inflation is in place whereby all sorts of news are given the "breaking" epithet, and apparently are worth a 45-minute block of coverage.

On reflection, this covergence makes sense. People stop paying attention to commercials, so they are made to look deceptively like news casts. People stop paying attention to news, so they are made to look deceptively like fiction.

I guess the cause to look at here is that people get bored quickly of whatever is placed in front of their eyes. Corporations (bound by the need to maintain popular interest in order to stay profitable) scramble to keep you from turning the TV off or switching the channel, losing in the meantime sight of the goal. Given that corporations are profit-seeking, this is the right strategy. So why do people get bored? Why do we need "more" and more each time to maintain a constant level of interest?

I believe that getting "bored" is a fact of life, an artifact of being human. We have memory so we compare (time-adjusted) outcomes yesterday to outcomes today. This is what I would call the desire for progress and I don't think this is bad per se.

Where our tendency to get bored becomes a problem, though, is when we realize I think that our society today (which, unlike human nature, is not constant) has the tendency to value instant gratification. Now don't get me wrong-I see a lot of people make this mistake-there is nothing inherently bad, or evil about instant gratification. This need, in my opinion, can be fundamentally linked to the uncertainty about one's future and life purpose (either because one supposes that one needs to live an extremely rich life to find purpose, or takes a resigned view and decides to grasp the moment). The problem with instant gratification, though, is that it it a very costly life philosophy. You trade higher utility today for higher utility tomorrow-each decision you make is local: your one life decision doesn't affect any other. You don't invest. Because there is no room for investment in life, the only way to get valuable output is to put a lot in. Since we get bored, this process gets less efficient as time goes on: next time we put in the same amount, we receive slightly less output. This means either we're destined to be ultimately depressed, or go crazy trying to put more and more in.

Using money to make oneself happy is a good example: you need to continue spending more and more because you remember what you bought before and how that made you happy. That was some time ago so, time-adjusted, you now need to spend more to maintain the same utility. You end up spending ridiculous amounts of money just to be as happy as you were when you bought your first Matchbox toy car as a young child.

Is there an alternative? Yes, it is either to address the problem with instant gratification, or change your philosophy. The former is very hard- I think instant gratification works if you an inexperienced and have the potential to put a lot more in than you expect to receive. This is why children like-and should be offered- instant gratification. Later in life, as you get more sophisticated, you really need to change your philosophy. I recommend learning to be patient, investing.

What is causality?

October 07, 2009 by Lukasz Strozek

As I re-watched fragments of Benjamin Button recently (a movie that I’m not particularly fond of, I’m afraid), I recalled a scene in which a particular incident was shown to be preceded by a series of events that took place that ultimately led to it. If at least one of these events had not happened, the narrator argued, the incident could have been avoided. This got me thinking about causes and what it really means to call something a “cause” of some event (more narrowly, how one assigns “blame” to things, or gives credit to things).

As we can easily predict, there is often no single cause of an event. WARNING: spoilers abound! Even though the driver, who struck Daisy, seems like he was the cause, if many other things hadn’t happened, Daisy would have been fine; shouldn’t those other things also be considered causes? How far back do we go? How do we attribute causality–it seems to us, viscerally, that some factors were more instrumental to the incident than others, but how do we quantify that? (For example, the invention of the automobile was among the causes but was it as significant as the fact that the driver didn’t pay attention to what was in front of him?).

This is a difficult question and so let’s start small. The universe is massive, with so much happening in such short periods of time that it’s easy to get confused. Let’s simplify the question as much as we can (it’s still going to be pretty complicated so bear with me).

I’m going to assume that the universe consists of a series of discrete decisions that lead to some event. The decisions are binary (and let’s assume that the choices are 0 and 1–whatever these numbers may stand for. For example, 0 may mean “forget the jacket” and 1 may mean “take the jacket”) and could stand for anything that has two distinct outcomes, so I’m using a broad definition of the word “decision” here. We will try to come up with some framework that allows us to talk about these decisions–for example, determine which decisions contributed to the event more than others. First, some caveats:

We will not deal with intent, that is, we will not be interested in what a particular decision intended to achieve and instead look at what it ended up achieving. This means we’ll be looking at cause in a way which may be different from the way the law looks at cause.
We will deal with decisions which are not biased in any way, i.e. behind each decision there is an agent who is either picking 0 or 1, and is not subject to chance. Hence, a “decision” to rain in Sahara is not a valid one since it’s not particularly likely to rain in Sahara.
We can model decisions which are biased, or decisions which are not binary, as a sequence of binary decisions, so we can proceed without loss of generality (I never thought I’d use this phrase again…)
We’ll assume that all decisions are discrete, that we can determine the consequence of every decision and that we have captured them all

Moreover, in order to talk about causality at all, we have to define equivalence of decisions and events properly. We’ll be dealing with parallel universes (i.e. universes in which a particular decision had been made differently) and, strictly speaking, events across universes are never the same (because the universe is slightly different if a decision is made differently, even if it seems that a particular event was not at all affected). We will identify an equivalence class of events (and equivalence classes of decisions) — buckets, where we put many similar events and treat them as the same, as the event.

For example, consider the event “Daisy breaks her leg as a result of a car accident”. If, in a parallel universe, some decisions are made differently, and Daisy breaks her other leg, the event is now different, but we still care about it (for all intents and purposes, she’s broken a leg). So we’ll put the two events in the same equivalence class. Similarly, the driver’s decision to not pay attention should be treated as the same decision regardless of the decision to forget the jacket, so we need equivalence classes of decisions.

Let’s work with an example. Consider three decisions \(d_1\), \(d_2\), \(d_3\), that led to some event \(E\). We can represent this as a tree of decisions:

The graph represents the current universe — the three decisions were made, and the event \(E\) happened. Now let’s introduce parallel universes — let’s determine what would have happened if either of the decisions had been made differently. Suppose that if \(d_3\) was 0, \(E\) could still have happened if two other decisions \(d_4\) and \(d_5\) were 1. If \(d_2\) was 0, there is no way for \(E\) to happen. If \(d_1\) was 0, \(E\) could happen if \(d_3\) was 1 and a new decision \(d_6\) was 1.

This is, of course, arbitrary — in the real world it may be difficult if not impossible to reason about what would have happened. But there again, I never made any claims about the practicality of this framework…

Note that in our example above decision \(d_3\) is reused: it appears in the parallel universe as well as in the actual one. This is fine — a decision may appear in many universes (especially if decisions are unlikely to influence one another, for example, because they happen far away from each other). This is also why we need equivalence classes of decisions (so that we can talk about similar decisions rather than treating every decision as a unique one). Those “reused” decisions will be tricky to analyze: on one hand, they are the same decision, so we could talk about it in the abstract, regardless of what our universe looks like (i.e. regardless of what decisions have actually been made); on the other hand, by the time a decision needs to be made, other branches of the tree (that may include the same decision!) can be pruned. We’ll solve this problem shortly.

We can complete the decision tree:

Now we can look at all combinations of different decisions and see if \(E\) occurred or not (\(x\) means “any value”):

2 3 4 5 6	  E?      # distinct combinations
x 0 x x x	  0	  16
x 1 x x 0	  0	  8
x 1 x x 1	  1	  8
0 x x x x	  0	  16
1 0 0 x x	  0	  4
1 0 1 0 x	  0	  2
1 0 1 1 x	  1	  2
1 1 x x x	  1	  8

For example, if \(d_1\) was 0, \(d_3\) was 1 and \(d_6\) was 1, the event happened regardless of the values of the other three decisions (and there are 8 such combinations).

Now we can compare the decisions and see which one caused \(E\) the most. For each decision, determine for how many combinations \(E\) happened, and for how many it didn’t (if a decision didn’t matter for the outcome, for example \(d_2\) in the case when \(d_1\) is 0, we can exclude the scenario from our calculations). The difference between these two numbers is the extent to which that decision caused \(E\). For example, if \(d_1=0\), \(E\) is caused in 8 out of 32 combinations. If \(d_1=1\), \(E\) is caused in 10 out of 32 combinations. So regardless of \(d_1\), \(E\) is caused in at least 8 out of 32 combinations (so that much wasn’t caused by \(d_1\)). However, the remainder — 2 out of 32 combinations — were caused directly by \(d_1\) so the causality of \(d_1\) is 2/32 = 1/16.

Similarly we can compute the causality for the other decisions:

\(d_2\): if equal to 0, causes \(E\) in 0 combinations; if equal to 1, causes \(E\) in 10 out of 16 combinations. So its causality is 5/8
\(d_4\): causes 0 if equal to 0; 2 out of 4 if equal to 1. Its causality is 1/2
\(d_5\): causes 0 if equal to 0; and all (2 out of 2) if equal to 1. Its causality is 1
\(d_6\): causes 0 if equal to 0; and all if equal to 1. Its causality is 1

Let’s now look at the tricky case — \(d_3\). It appears in two branches of the tree. The answer to how much it caused \(E\) will depend on how much the agent making the decision knows about the decisions made up until now (specifically, \(d_1\) and possibly \(d_2\)). In other words, if the agent knows which branch of the tree he is in, he’s causing \(E\) to a different degree than if he had no such information.

If the agent has no information, we need to look at all combinations. If \(d_3\) is equal to 0, \(E\) is caused in 2 combinations out of 24; if it’s equal to 1, in 16 out of 24. Its causality is 7/12
If the agent has perfect information, we need to consider which branch of the tree he’s in.
If he’s in the right branch of the tree: if the decision is equal to 1, \(E\) is always caused. Otherwise, \(E\) is caused in 1 out of 4 combinations. The causality is 3/4.
If he’s in the left branch of the tree: if the decision is equal to 1, \(E\) is caused in 1 out of 2 combinations. Otherwise, it’s never caused. The causality is 1/2.

Hence \(d_5\) and \(d_6\) cause \(E\) the most (which makes sense: since they are at the bottom of the graph, they have full control over whether \(E\) happens or not). \(d_1\) causes \(E\) the least. However, it’s not always true that the higher up the tree a decision is, the less it contributes to the event: \(d_2\) contributes more than \(d_3\) (with no information).

My idea of a top job

October 05, 2009 by Lukasz Strozek

Most of us want to do meaningful work; we want it to be impactful and we want a lot of responsibility. And, in fact, as we get older, we tend to acquire more responsibility and move from a position that doesn’t really matter for anything to a position that matters a great deal. That got me thinking about jobs in the abstract, what it really means for work to be impactful or meaningful, how companies should pay their employees, and–perhaps in a kind of a gedankenexperiment–what a job would look like if we took this progression to an extreme.

I realized at some point that in a well-functioning company, decisions are much better indicators of responsibility and impact than actions (there are a few exceptions to this, where a person’s (say, a master artisan’s) skills are so unique that they are worth vast amounts of money). Decisions have a much more far-reaching implications than actions because in a well-functioning company, actions can be delegated or outsourced; and there is a large number of people who have similar skills.

Hence, I like to evaluate the meaningfulness of work by treating it as a series of decisions and assessing the impact of each decision. Everyone makes decisions in their work. A graphic designer decides what color the cover of a book should be. A computer programmer decides which pattern to use in his/her piece of code. CEOs decide who to hire for the top management echelon of the company. Naturally, the impact of their decisions varies: if a computer programmer makes a decision to use a particular pattern, he or she may make it slightly more difficult to alter the program in the future. This one can, theoretically, translate to some amount of money that the company could save (or waste). Similarly, if a CEO makes a decision to hire a particular person, that may have far-reaching implications (which could also be, albeit rarely if ever is practical to be, assessed in monetary terms). You can compare the impact of these decisions–and thus define the responsibility a particular employee has.

Taking this to the logical extreme, I imagine a person sitting in an oversize leather chair, in the middle of a mildly dark room. That person doesn’t talk to anyone, doesn’t have to go anywhere. Every few hours somebody enters the room with a piece of paper and passes the paper to that person. That person reads what’s written on the piece of paper and either nods or shakes his head. The messenger leaves. That’s all that this person does all day.

While it may seem like a scene from some kind of movie (in fact, many movies do play with this concept), it makes sense to me. We can reduce decisions to a series of binary decisions, requiring nothing but a nod of one’s head. We can eliminate all actions from that person’s responsibilities because all actions have been delegated many, many levels below. The person doesn’t need to attend any meetings: the employees one level below do what’s necessary (which may include having plenty of meetings) to distill the work that’s required to a small set of binary decisions. In fact, if you think hard, you’ll probably see that a lot of decisions that you made or see other people make at work can be characterized very concisely; one fundamental decision leads to a series of smaller decisions (which there are many of, but which are easier to make so our Top Guy wouldn’t ever be bothered by them). In fact, many CEOs do something like this today, but their jobs are still not pure exercises in decision-making: they have to attend meetings, write emails, talk to people.

We can see how this Top Guy’s job involves more responsibility than anyone else’s. Even more: his job involves more responsibility that everyone else’s jobs lumped together. His decisions percolate to the bottom of the company, affecting, ultimately, all employees. The fact that a decision was escalated to him means that it was deemed important enough such that nobody below him could make that decision, even when cooperating with others.

What a sweet job to have.

Backwards-compatible electrical outlets

September 29, 2009 by Lukasz Strozek

Spot the difference between these two outlets:

The one on the right has a T-shaped slot in place of one of the two blades. As everything in engineering, this is not random. This extended slot gives you (or should be giving you) useful information about your electrical connection. It turns out that an outlet with a T-shaped slot is configured to feed up to 20 amps of current while the regular two-blade outlet can guarantee at most 15 amps (of course, if the outlet is not installed to code, this may not hold).

What I like about this, though, is that the 20-amp outlet is backwards compatible for devices that don’t need as much power, i.e. you can plug in a device that only needs at most 15 amps into a 20-amp outlet (which is fine, an outlet will give you as much current as you need, up to a limit). However, you can’t do the reverse, i.e. plug a device that needs 20 amps (presumably if I equip a device with a plug with a T-shaped prong, I’m claiming that 15 amps is not enough) into a 15-amp outlet — its plug will simply not fit into a two-blade outlet! This is a great safety feature.

Unfortunately, it doesn’t seem like the more advanced outlets follow the same convention.

True vs Compensated qualities

September 28, 2009 by Lukasz Strozek

I’ve always thought of myself as a very organized person, to the point of slight compulsive behavior. I make lists of things to do (as a one-off, every week, or asap); lists of things done; lists of thoughts I’ve had; lists of sites I like visiting; lists of quotes, etc. I have great systems for keeping myself organized that ensures I never forget anything and allows me to prioritize my tasks.

I had a conversation with one of the companies that do personality trait assessment. Usually I don’t find these things particularly useful–anything they tell me I could have told them initially (since I know my strengths and weaknesses well); moreover, the answers they give me are usually limited at trying to get me to realize my strengths and weaknesses (which I already do) and carefully try not to offend me (which is a waste of time since it’s really difficult to offend me). However, there was one thing these guys said that made me stop and think. They said that my great organizational skills and the ability to manage large lists of tasks in the right order are just a way for me to compensate for my natural drawbacks in these areas. In other words, I’ve constructed an elaborate workaround for my problem, to the point where even I believe that I’m efficient.

The interesting thing is, I have no way to prove whether they are right or not (since there is no good test on where your personality traits come from) but I accept the possibility they are right. This allows me to think about some things I could do if they were right that would address the root part of the problem. These root problems are useful to squash, because it’s likely they will cause other problems (not the hypothetical one) later on. In the face of the absence of information, we have to make the most educated guesses and try to precompute what makes sense to precompute.

Encore and Standing Ovations

September 24, 2009 by Lukasz Strozek

These are good examples of what I'd call "the inflation of the public's expression of enthusiasm" that has been in place ever since the "Encore!" call and standing ovations started to be used as devices for the public to express their approval of the artist.

Standing ovations would be used in special circumstances, when the artist's performance was so spectacular it deserved an expression of gratitude and approval much higher than applause. Often only a subset of the audience would bestow standing ovations, since an opinion of excellence in the area of public performance is no doubt a personal one.

Today standing ovations are given very liberally. Worse still, you just need a "critical mass" of people to stand up and suddenly the entire room stands up. I stand up because the idiot in front of me just stood up and if I want to catch the last glimpse of the performers, I don't have much choice but to stand up thus contributing to this wave of inflated opinion.

Encore is even more interesting. Again, when the public took a particular liking to a performance, its members would collectively call "Encore!", asking for more. The artist would oblige. Today, not only does the artist perform an encore almost every single time; the public has in fact stopped asking for it, as if there was some kind of secret hand shake that happened between the collective body of all performers in the world and all the audiences in the world.

I don't have a big problem with it (a little bit of inflation is generally a good thing) unless the resource that is subject to inflation is bounded. In case of money, something can always cost a little more (I have the cardinality of natural numbers to thank for this, I guess--maybe Peano, maybe Cantor, I don't know). But I don't really have much of a choice when it comes to performances. What am I going to do if the performance has been truly spectacular? Am I going to stand on the chair? (I considered throwing roses but that seems archaic, and the logistics!--I would have to have bought roses ahead of time just in case the performance was good; such heightened expectations make it more difficult to really overwhelm me with a performance... lots of problems)

In the case of encore this inflation has reduced to an awkward (to an objective observer that happened to have been on Mars for the past thirty years, I guess) routine where the artist finishes his or her performance early (because they must leave the best piece for the end!), waves everyone goodbye (nowadays this also happens pretty lazily since everyone knows it's not the real goodbye), and then comes back after a minute or so (what do the artists do in that time? Enjoy their much-needed respite?). We live in a funny world indeed.

The Metropolis

September 21, 2009 by Lukasz Strozek

Last weekend my friend and I sat on a rooftop of a building in New York City. I marveled at the sights and even took a picture with my bad camera (when are you going to get better, oh iPhone camera?) so I wouldn’t forget those few hours I spent pondering the future of mankind.

There are some skyscrapers, but surprisingly the view was dominated by relatively short (six- or seven-story) buildings. The picture doesn’t do it justice at all, of course, but you can see some of them in the foreground. My friend called these structures “ugly” and continued looking at the skyscrapers. Then it dawned on me that those very “ugly” buildings represent a dying era; and the skyscraper, spread in a gridlike fashion, omnipresent, dominating, commanding, looking down on you, is a harbinger of a new age. The age of the Metropolis.

What’s the difference, you’ll ask. The differences are subtle, but that’s how changes happen, through a deluge of subtleties. I could imagine–I nearly saw it unravel in front of me–how in the near future, the skyscraper will be everywhere. Wherever you look, you’ll see a wall. It won’t matter that you’re in a high-rise building, because all the buildings around you will also be high-rise. Being on the fiftieth floor will be indistinguishable from being on the second. The rooftop, perhaps the last standing symbol of the old days, will cease to exist as increased security and–quite frankly–unremarkable sights discourage landlords from opening it to the public.

The differences are even more apparent if you close your eyes. The late-twentieth Century City (let’s settle on such a name for the passing era) is alive. You can hear everything that’s happening in the City while sitting right there on the rooftop. The sirens of emergency vehicles dozens of blocks away get transformed as they bounce off the irregular structures; the sound interferes with itself as it diffracts off the buildings. What reaches your ear is a remarkable narrative compression of the inner workings of the City, a true symphony. I encourage you to try the same — go somewhere high enough so thenoise of the city starts blending into music.

What will replace this symphony in the new era? Silence. The new era has no need for noise. Everything is hermetic, sealed off from the world. You can’t even make out what is behind that tinted glass. The emergency vehicles will cease to exist as well: in a well-engineered Metropolis, all emergencies are taken care of locally (plus, it would be impossible for emergency vehicles to get anywhere in the Metropolis). Maybe they will be kept around to appease the tourists who will walk through a Times Square and want to experience the thrill of an emergency, a sudden rush of blood as an ambulance passes by. How will schoolchildren learn about the Doppler effect?

The 1927 movie “Metropolis” comes to mind. At first glance it may seem obsolete–that’s not that the future looks like!. But if you watch it more closely, you’ll see that it’s closer to what the future will bring than you think. If we simplify things and assume there are discrete eras in the evolution of Man, and that we’re living in era n, we’ll notice that eran+1 is heavily influenced by the current era (which was heavily influenced by era n-1). The Skyscraper, for example, is really an invention of the twentieth Century. What the movie “Metropolis” (which was arguably made in era n-2) does is describes era n+2, an era which we cannot even begin to comprehend, a City that’s distant, remote, un-human. It’s a City that we don’t want to be part of. Finally, it’s a totally silent City.

I was saddened by the thought that my friend, who today calls the artifacts of the near-bygone era “ugly”, will in just a few decades struggle to convey the magic and mystery of the late-twentieth Century City to his children. No wonder though–the new age will maximize the probability of its success, even if it means vilifying, banishing, destroying the old one before its time comes. And looking at my friend–a covert (though he doesn’t know it) agent of the new age–the probability of its success is high indeed.

Crowdsourced Art

September 19, 2009 by Lukasz Strozek

(Originally published September 19, 2009; Updated on September 16, 2013)

Inspired by this guy I thought of something that might be fun to do: have the community generate a small image collaboratively by allowing everyone to paint a small part of it. In a way, I wanted to crowdsource the generation of a computer graphic. This became my miniproject for the past weekend, and also a good way to announce the Grand Opening of this site (until now nobody really knew about it).

The idea is quite simple: consider a 67×67 pixel image. It’s pretty small, but sufficient to capture quite a lot of detail, e.g.

A lot of detail can fit in a 67x67 image

The image starts fully transparent. I then give away tokens to people I know; each token gives the owner the right to put a small number of pixels (say, 15) on the image. Everyone is free to pick what colors each of the pixels should be, and which pixels to set. If I give away enough tokens, and if people want to participate, interesting results can be generated (all without my involvement at all!)

I’m going to make this a little more fun by introducing two rules:

You can "draw" over other people's pixels but that’s going to cost you more (2 pixels instead of 1) — this is to imitate what artists do, often painting over sections of their image multiple times
You are rewarded for collaborating with others. If two people get together, they can "merge" two tokens into one, and, just like a two-liter Cola costs a little less than two one-liter Colas, such combined token allows you to draw more pixels than what the original tokens allowed. (Similarly, splitting a token into two pieces is allowed, but the resulting two pixel “allowances” will add up to a little less than the original).

The second rule is, in my view, particularly interesting and I expect some fascinating results. Since one person needs both tokens to get the combined one, you must trust whomever you're giving your token to. You can, of course, just give up your rights to drawing pixels and give your token to somebody else. Perhaps you can work out some kind of deal with your friend (I don’t know how much a pixel is "worth"; the whole idea is to encourage collaborative creativity and not make somebody money but, as I said, I don’t want to control what will happen).

The first rule is interesting, too, as the image fills up and people decide to paint over other people’s work. Perhaps there are parts of the image that don't fit aesthetically with the rest. It could get personal! Or, the canvas is full but people still have tokens left.

To make it a fun and lasting exercise I'll be giving tokens to people going forward (not just in the initial batch), perhaps for commenting on this blog? (ah yes, brownie points for participation...)

You can check out the work in progress here. I tested the site with Chrome, Firefox and Safari on the Mac, and I'm pretty sure that Windows and various flavors of Linux work as well. If not, let me know, or better still, submit a patch.

If I haven't sent you an email with a token, let me know and I'll throw something in.

(Update: September 24, 2009)

The work so far is fun to look at; undisputedly predictable was the penis that found its way on the canvas a few hours after the game started, but there have been efforts to turn it into a happy face (I must admit, I was tempted to use up some of my tokens but in the end I decided this piece of art is a no judgment art and anything goes).

An interesting pattern was that people used the background image and the fact that the canvas was translucent to trace elements of the image onto the canvas. I did not expect that, but I guess that's an as good place to start as any.

Finally, people are not taking advantage of the collaboration element of the game. I'll let you in on a secret: the "bonus" you get for merging tokens is actually pretty substantial. In fact, the number of pixels you can set is equal to the "size" of the token (the first three digits) raised to the power 1.25. This may not seem much, but consider merging two tokens, each of "size" 10. Each individual token allows you to set 10^1.25 = 18 pixels, so in total both tokens let you set 36 pixels. If you merge the tokens, you will get one token of size 20 and 20^1.25 = 42 (you've just gained 6 pixels). The differences are even larger for larger tokens (or more tokens). Two tokens of size 20 give you 84 pixels when separate and 101 when merged. You get the idea.

(Update: September 16, 2013)

The first iteration of this project yielded the following image:

The result from the first, 2009 experiment

I'm running another iteration, this time opening it up to a much larger community (400+ people) and letting anyone mine for tokens (so long as they stay on the website for long enough). I updated the code a little, taking advantage of canvas rather than doing all graphics on the backend, which used to make for a poor user experience.

I also allow people to mine for tokens, so long as they stay on the page. The idea is similar to bitcoin mining, where the server sends a challenge hash and the client must find a value that hashes to the challenge. In this case, the client is the browser. I set the challenge up so that in 30 minutes, you are 50% likely to find one pixel-worth of a token. Assuming you find the token, the expected amount of time to wait until you mine it is 15 minutes.

Do you buy lottery tickets? No? Think again.

September 17, 2009 by Lukasz Strozek

Some of us are appalled at the idea of buying lottery tickets. The chances of winning, you might say, are so slim (not mentioning negative expected value) that I'd much rather buy a beer to boost my utility. And it might be quite rightly so -- the lottery benefits mostly from people who don't know basic probability theory, find it difficult to internalize really large or really small numbers, or are simply risk-loving.

But if you swear you would never willingly participate in a lottery, think again. I will reveal a secret to you. Granted, this is somewhat of a simplification, I'll admit, but one that has some merit nonetheless.

The chances are, you have been to a doctor. Any doctor, say, a dentist. You may even have complained at the amount of money you had to pay for service. When you consider what goes into the money you pay, you start separating out the doctor's honorarium, the cost of the supporting staff (the ladies in the reception that know your name when you enter the office), the cost of the office itself (and the magazine subscriptions); more indirectly, the cost of the bureaucracy required to sustain the insurance program you're subscribed to (and yes, the cost of these statements you get in the mail), and so on. One of these myriad hidden costs struck me as very surprising -- it's the cost of a lottery ticket!

How so? We live in a culture of litigation. People love to sue other people, perhaps in a modern manifestation of bullying (which really is in the human nature), perhaps as a gamble (many people I'm sure think they can "cheat" the system), perhaps out of some conception of social justice using as its medium the one truly universal, fully transferrable, comparable and quantitative measure of your fit as a member of the society -- money.

We most often sue medical practitioners, probably because we go to various kinds of doctors a lot, because the doctors perform work closest to what we hold the most dear (our bodies), or because our bodies are enough of enigmas to allow us to stand our argument in court (it's not like an expect can measure how much it hurts in some truly universal, fully transferrable, comparable and quantitative measure -- ironically, however, we do believe that we can measure the compensation we should get in the very same unit). It's just a fact of life.

Doctors know this, and they know that those lawsuits are a kind of an act of randomness. It's never clear what circumstances may cause a patient to decide to sue (to be fair, I'm not exonerating medical practitioners -- it's quite possible that the lawsuit is due to a legitimate error, malpractice, or gross negligence!). To ease their life, doctors buy legal insurance -- it's just like life insurance, but it allows the doctors to protect themselves from the costs of lawsuits for a low monthly fee. This is smart -- it reduces the risk as seen by the doctor, given that lawsuits do happen.

Now the punchline -- guess who's paying for this low monthly fee! Great lottery you're part of...